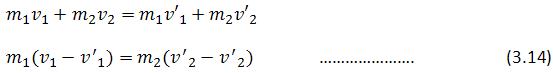When two tennis balls collide then, after collision, they will rebound with velocities less than the velocities before the impact. During this process, a portion of K.E is lost, partly due to friction as the molecules in the ball move past one another when the balls distort and partly due to its change into heat and sound energies.
A collision in which the K.E of the system is not conserved, is called the inelastic collision.
Under certain special conditions no kinetic energy is lost in the collision.
In the ideal case when no K.E is lost, the collision is said to be perfectly elastic.
For example, when a hard ball is dropped onto a marble floor, it rebounds to very nearly the initial height. It looses negligible amount of energy in the collision with the floor.
It is to be noted that momentum and total energy are conserved in all types of collisions. However, the K.E. is conserved only in elastic collisions.

Elastic Collision One Dimension
Consider two smooth, non-rotating balls of masses m1 and m2, moving initially with velocities v1 and v2 respectively, in the same direction. They collide and after collision, they move along the same straight line without rotation. Let their velocities after the collision be v’1 and v’2 respectively, as shown in Fig. 3.9.
We take positive direction of the velocity and momentum to the right. By applying the law of conservation of momentum we have
As the collision is elastic, so the K.E is also conserved. From the conservation of K.E we have
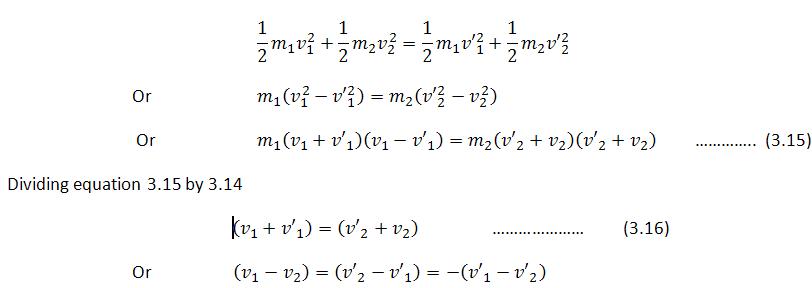
We note that , before collision ![]() is the velocity of first ball relative to the second ball. Similarly
is the velocity of first ball relative to the second ball. Similarly ![]() is the velocity of the first ball relative to the second ball after collision. It means that relative velocities before and after the collision has the same magnitude but are reversed after the collision. In other words, the magnitude of relative velocity of approach is equal to the magnitude of relative velocity of separation.
is the velocity of the first ball relative to the second ball after collision. It means that relative velocities before and after the collision has the same magnitude but are reversed after the collision. In other words, the magnitude of relative velocity of approach is equal to the magnitude of relative velocity of separation.
In equations 3.14 and 3.16, m1, m2, v1 and v2 are known quantities. We solve these equations to find the values of v’1 and v’2, which are unknown. The results are


There are some cases of special interest, which are discussed below:

In this case the mass m2 be at rest, then v 2 = 0 the equations 3.17 and 3.18 give

When m1 = m2 then ball of mass m1 after collision will come to a stop and m2 will take off with the velocity that m1 originally has, as shown in fig 3.11. thus when a billiard ball m1, moving on a table collides with exactly similar ball m2 at rest, the ball m1 stops while m2 begins to move with the same velocity, with which m1 was moving initially.

(iii) When a light body collides with a massive body at rest
In this case initial velocity v2 = 0 and m2 >> m1. Under these conditions m1 can be neglected as compared to m2. From equations 3.17 and 3.18 we have v’1 = -v1 and v’2 = 0
The result is shown in Fig 3.12. this means that m1 will bounce back with the same velocity while m2 will remain stationary. This fact is made used of by the squash player.

(iv) When a massive body collides with light stationary body
In this case m1 >> m2 and v2 = 0 so m2 can be neglected in equations 3.17 and 3.18. this gives v’1 _ v1 and v’2 _ 2 v1. Thus after the collision, there is practically no change in the velocity of the massive body, but the lighter one bounces off in the forward direction with approximately twice the velocity of the incident body, as shown in Fig. 3.13.

Example 3.4: A 70 g ball collides with another ball of mass 140 g. the initial velocity of the first ball is 9 ms-1 to the right while the second ball is at rest. If the collision were perfectly elastic what would be the velocity of the two balls after the collision?
Solution:

Example 3.5: A 100 g golf ball is moving to the right with a velocity of 20 ms-1. It makes a head on collision with an 8 kg steel ball, initially at rest. Compute velocities of the balls after collision.
Solution: we know that

Do you know?